
Quando si parla di piegatura, in particolare di pressopiegatura, si pensa a una lavorazione apparentemente semplice, ma che può nascondere molte insidie.
In questo articolo inizia un viaggio nella teoria della piegatura, toccando diverse tecniche utilizzate negli anni, alcune delle quali ancora in uso, per prevedere il comportamento di una lastra metallica durante la deformazione.
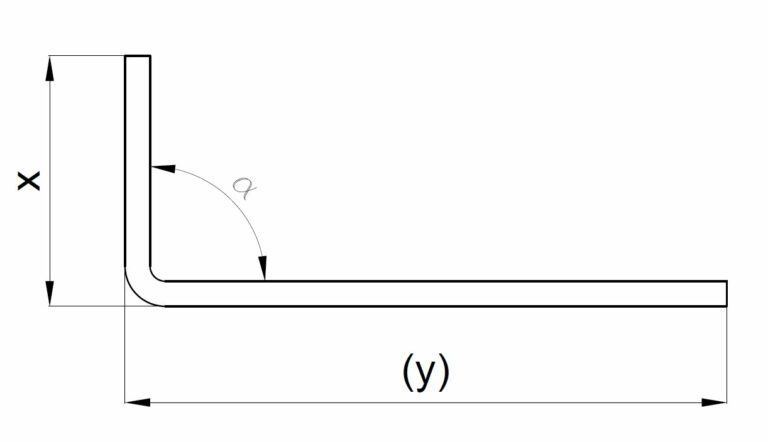
Figura 1 – Cosa si ricerca durante la programmazione di una piega
Riducendo il processo ai minimi termini, possiamo dire che un operatore, nella fase di programmazione del controllo numerico della macchina, cerca essenzialmente due valori: un angolo e una lunghezza di flangia “x” (figura 1). La lunghezza “y” è una conseguenza, tanto più precisa quanto è stato accurato lo sviluppo del pezzo durante la fase di progettazione.
Da un punto di vista matematico, esistono molti altri valori che, nel corso degli anni, sono stati impiegati per creare formule geometriche utili a prevedere gli sviluppi in maniera più affidabile possibile.
Tuttavia, utilizzare un approccio puramente teorico non garantisce sempre affidabilità al 100%. Il metodo più efficace è combinare tali criteri con tecniche di reverse engineering, cioè verificando i risultati reali attraverso test specifici che riproducono le condizioni di lavoro: spessore, materiale, utensili e senso di laminazione (quando sono richieste alte precisioni su materiali anisotropici).
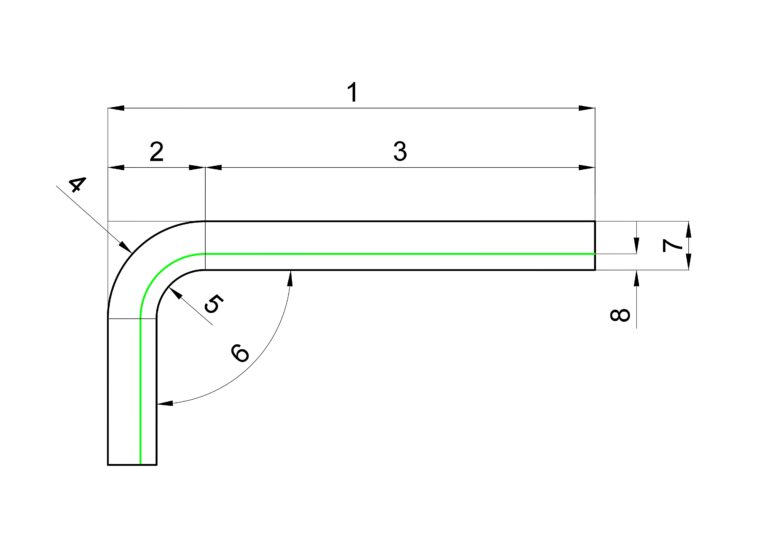
Figura 2 – Parti di una piega
Quali sono le parti di una piega?
Di seguito elenchiamo e definiamo ogni singola parte di un pezzo piegato, come illustrato in figura 2:
- Flange (flangia): rappresenta la misura esterna della piega.
- OSSB (outside setback): la distanza tra l’inizio del tratto deformato e lo spigolo esterno della piega.
- Leg: il tratto rettilineo tra la fine del pezzo e l’inizio del tratto deformato.
- OR (outside radius): il raggio esterno della piegatura.
- IR (inside radius): il raggio interno, uno dei valori fondamentali per calcolare gli sviluppi.
- B< (bend angle): l’angolo di piega.
- Mt (material thickness): lo spessore del pezzo.
- t (offset of neutral axis): la distanza tra la superficie interna e l’asse neutro del pezzo.
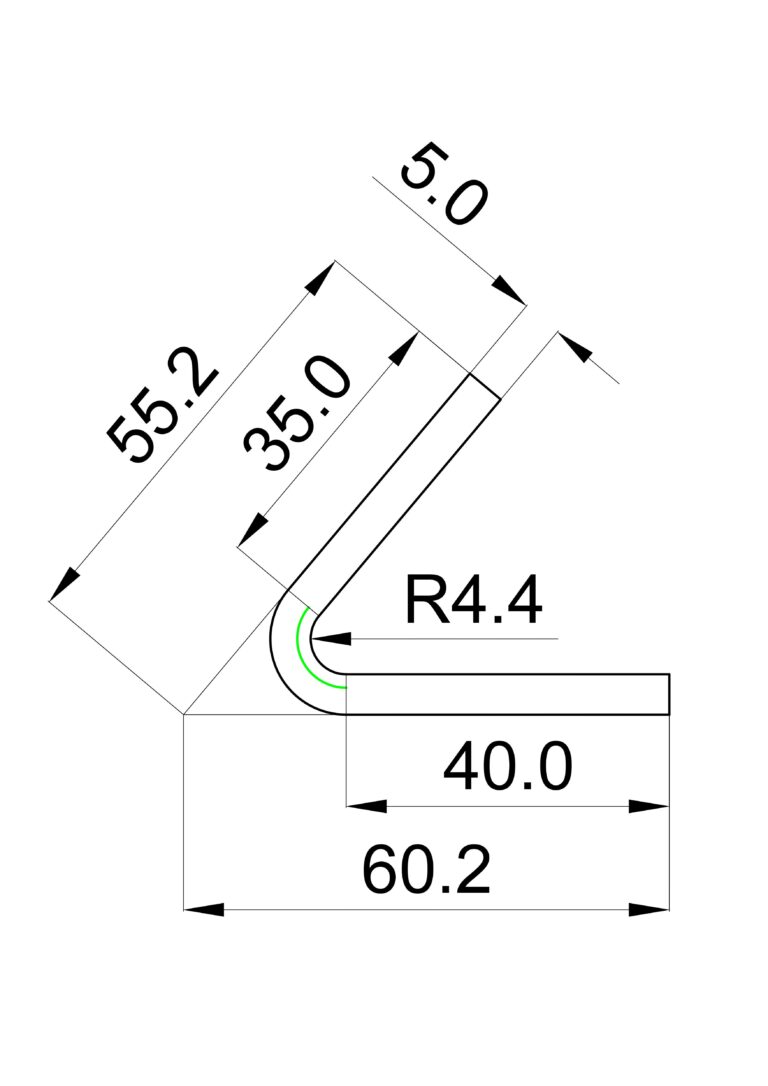
Figura 3 – Riferimenti con la bend deduction
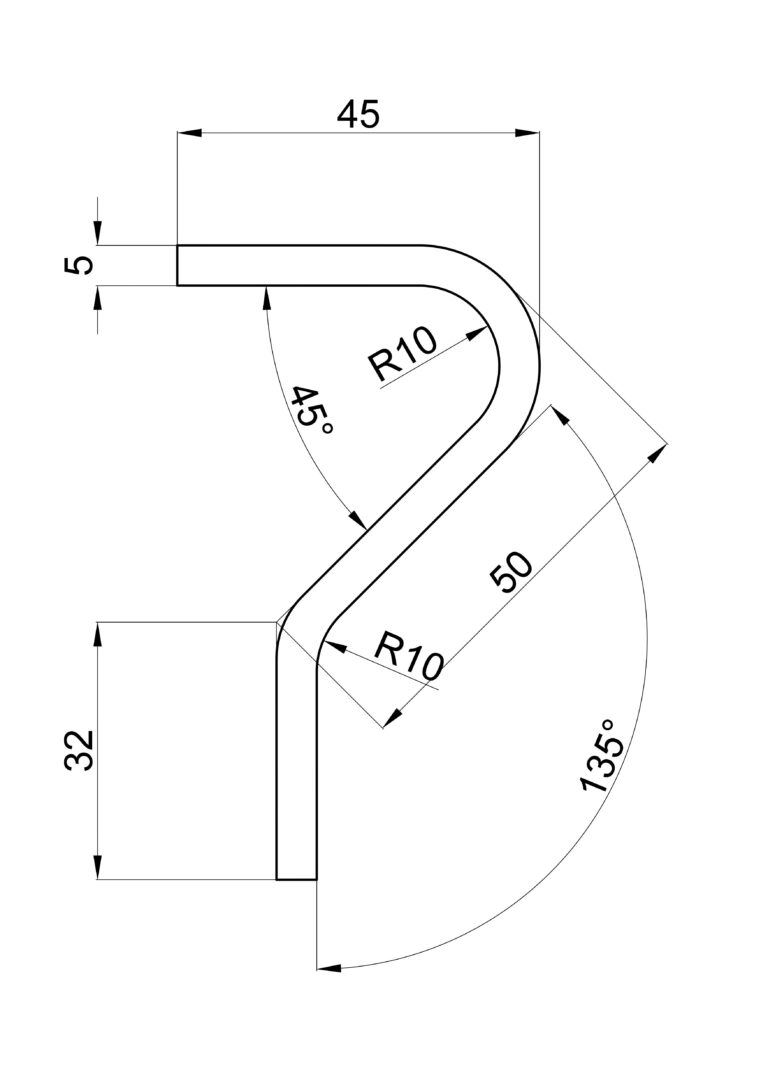
Figura 4 – Riferimenti con approccio delle norme DIN
Quali sono i riferimenti?
La scarsa letteratura sulla piegatura della lamiera mostra spesso formule matematiche basate su pieghe di 90°, che possono generare incomprensioni. I “punti oscuri” derivano dai diversi riferimenti adottati dai vari approcci.
- Flange: in una piega a 90°, la misura della flangia è identica in tutti i sistemi, ma può essere ingannevole con altri angoli, specie se si utilizza l’approccio della “deduzione di piega” (bend deduction). Nel metodo DIN 6935, gli angoli acuti sono riferiti alla tangente del raggio esterno (figura 4).
- OSSB: varia a seconda dei metodi e sparisce per angoli inferiori a 90° secondo le norme DIN.
- Leg: il tratto rettilineo usato per il calcolo della “bend allowance” si basa sulla lunghezza dell’arco formato dal piano neutro.
- Raggio esterno: è il riferimento utilizzato per gli angoli acuti nel metodo DIN 6935.
- Raggio interno: dipende dal tipo di materiale e dalla larghezza della matrice. Questo è uno degli elementi che spesso causa incongruenze tra progettazione e realizzazione.
- Angolo di piegatura: nel metodo DIN 6935 si fa riferimento agli angoli interni, mentre nella “deduzione di piega” si considera l’angolo supplementare, ovvero la differenza tra 180° e l’angolo interno. Ad esempio, per una piega di 45°, l’angolo nel metodo della deduzione di piega sarà di 135° (180-45).
- Spessore del pezzo: rimane invariato tra i vari criteri.
- t: indica la distanza tra l’interno della piega e l’asse neutro ideale, valore essenziale per calcolare il fattore k, in quanto k = t / T.
Conclusione
Ogni parte di una piega ha un ruolo cruciale nel determinare l’esito finale della lavorazione. Sebbene i modelli teorici rappresentino un’importante guida, non possono essere considerati come soluzione definitiva senza risultati reali che ne confermino l’efficacia.
La precisione dipende non solo dai calcoli teorici, ma anche dalla capacità di adattare questi modelli attraverso prove pratiche di reverse engineering, confermando così l’affidabilità dei risultati.
Articolo pubblicato sulla rivista Lamiera edizioni Tecniche Nuove maggio 2021.
Hai bisogno di informazioni? Scrivi a emiliano@accademiadellapiegatura.it
Scarica gratis anche tu il nostro regolo di piegatura.
